I’m not like most people. I don’t love a good challenge.
However, I know that challenges are necessary for learning. And when I see a challenge in an online course, I get excited to see if I’ve retained anything until that point.
Quizzes are a great way to make sure your students are learning. And for a course creator, there’s nothing more important.
This is why we’re talking about how to create a quiz in your online course today (that doesn’t suck).
In today’s post, we’re covering:
- what makes a good quiz question (and how to write one)
- what types of quiz questions are most effective in your online course
- how often you should quiz
- what resources are available for adding quizzes to your online course
By the end of this post, you should have a good grasp of how to structure your quiz questions in your online course, what types of questions to include, and how to make them super effective for student learning.
Let’s get started!
Need a second pair of eyes on your online course? Get a proofreading quote for your course.
What Makes a Good Quiz Question?
The purpose of any good quiz question is to measure whether your student learned anything from your course lessons. Also, to determine whether your student learned enough.
For example, did your students learn enough in your lesson to recall that information later? Will they be able to put it into action at some point?
A good quiz question is dependent upon your course learning objectives. This is because your learning objectives are where the crux of your students’ learning is.
There’s no point in creating quiz questions that don’t have anything to do with the main learning objective of the course. Everything in your course should lead to your students learning what you want them to in the learning objective.
To determine student learning, you need to make sure your quiz questions relate back to your learning objectives.
How to Write a Good Quiz Question
Now that we know what makes a good quiz question, let’s write a few.
Let’s say one of your learning objectives is for students to be able to perform keyword research for a blog post. Your quiz questions should revolve around the necessary steps to get them there.
Some good quiz questions for this learning objective would be:
- How do you find the search volume for a keyword?
- What are 3 ways to find keywords people are searching for?
- What makes a good keyword?
Another really effective way of writing great quiz questions is to use Bloom’s Taxonomy. This can get a little more advanced, but I think it could prove really useful in your courses.
Basically, Bloom’s Taxonomy says that good quiz questions test the six levels of understanding:
- Knowledge: Create questions that let students recall facts, terms, and basic concepts (i.e., can you recall…?, how would you show…?).
- Comprehension: Create questions that let students organize, compare, or interpret, giving descriptors and main ideas (i.e., how would you compare…?, what is the main idea of…?).
- Application: Create questions that let students apply facts, techniques, or rules they’ve learned in a new way (i.e., how would you show your understanding of…?, what approach would you use to…?).
- Analysis: Create questions that let students identify motives or causes, make inferences, and find supporting evidence (i.e., what motive is there…?, what conclusions can you draw…?).
- Synthesis: Create questions that let students compile information in a new way or propose alternate solutions (i.e., how would you improve…?, what would happen if…?).
- Evaluation: Create questions that let students make judgments about information and validate ideas (i.e., what is your opinion of…?, how would you justify…?).
These are a few ways to write better quiz questions in your online course. You can learn more about how to write quiz questions using Bloom’s Taxonomy here.
What Types of Quiz Questions Are Most Effective?
Quiz question types typically vary, depending on what you’re teaching. There’s no right or wrong answer in terms of what quiz question types you MUST use.
Do what will get you the results you’re looking for from your students.
For example, if you have some time and want to create a thorough multiple-choice quiz that you can use over and over to quickly scan the results, then multiple-choice might work best.
Or, if you’d prefer more thorough responses, you might knock out a few short-answer questions that will take a bit longer to evaluate.
It all depends on how much time you have and what you’re looking for from your students. At the end of the day, you want to make sure you’re extracting valuable information that you can use from your students about your course. But also, you want to make sure they’re retaining and learning!
Also, keep in mind as you create your quiz questions, that you’ll want to provide immediate feedback to the user, wherever possible. If an answer is wrong, giving the user an immediate answer lets them see where they went wrong.
If you want to go further, include information in your feedback that points them to the exact lesson they need to review to get the question right.
For example:
At the end of the day, you have to decide what question type works best for what you’re teaching. Here are some basic guidelines you can follow when trying to determine what question type to use.
Short-Answer Quiz Questions
Short-answer questions are great if you want your students to remember facts, terms, or anything that can be written, from two words to two sentences.
The great thing about short-answer questions is that they require the student to actually think. They have to recall what they learned from memory.
You’re in a much better position for your students to show you what they’re learning with short-answer questions. They allow students to be flexible, as well as demonstrate their creativity in the course.
If you’re using short-answer questions in your course, be sure to:
- Use your own words in the question
- Make sure the questions are asking about specific problems
- Avoid trivia-type questions and long/complex sentences
What’s also great about this type of question is you can use it as a fill-in-the-blank question, too. If the answer to your short-answer question is one word, intentionally leave that word out for your students to fill in.
This is a good way to vary your short-answer questions, too.
Matching Quiz Questions
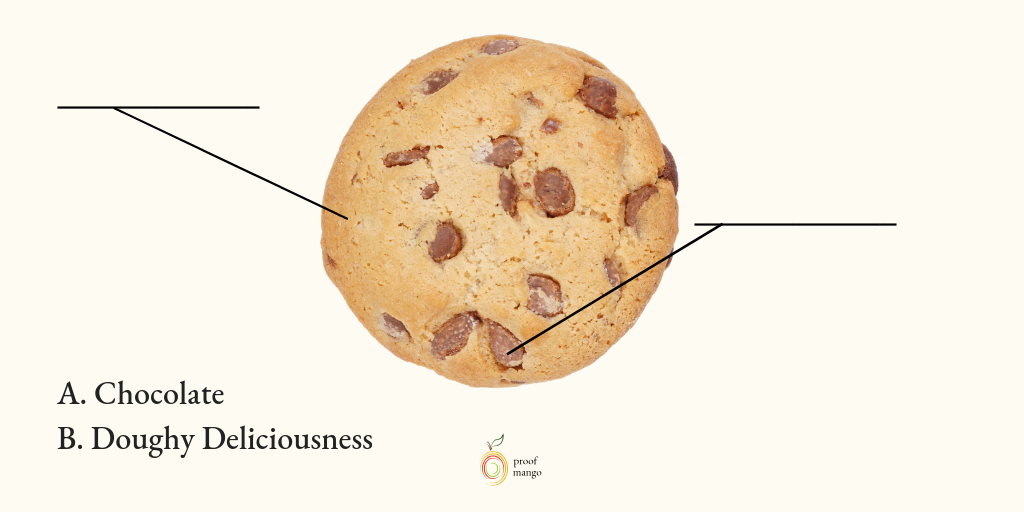
Matching questions are best used when you want to evaluate your students’ recall of more detailed knowledge. For example, if you want them to identify parts of an instrument, the body, or even a cookie.
You give them an image or graphic and list the terms that correspond to different parts of whatever is in the image or graphic.
These take students a little longer, but they’re easy to quickly grade and helpful in strengthening your students’ recall of detailed information. If you’re creating matching question types in your course, some things to keep in mind are:
- Make sure to keep your list items ordered (either chronologically or alphabetically)
- Try to make the list items contain the same type of information (make them all names, years, plant types, etc.)
- Keep your list items somewhat short and doable (10-15 items)
Essay Quiz Questions
Essay questions obviously provide you with more descriptive responses, because they’re longer. Usually, they ask a somewhat complex question and the students answer in an essay structure you set out (usually a 3-5 paragraph essay).
Most students cringe at the idea of an essay question. But online courses are great for this type of question, because students are usually in their own relaxed environment, with access to resources to help them out.
The evaluation process for this type of question is a little longer, and it may not apply to all courses. But at the end of the day, the answers you get from your students on these questions will be telling.
You’ll be able to really see how your students are integrating your material into what they already know. So you’ll get some great insight into how you’re teaching!
Some tips on writing essay questions:
- Give your students an option to choose from two essay questions, so they feel more comfortable
- If you can, give them a time limit
- Make sure your questions are clear and in your own words
- Try and use words like “compare and contrast” at the beginning of your questions
Multiple-Choice Quiz Questions
Multiple-choice questions are the most common type of quiz question, but they’re time-consuming to create. They also allow for “educated guesses”. But if that’s something you’re okay with, go for it!
When writing multiple-choice questions, best practices include:
- Making the incorrect answers look entirely plausible
- Including incorrect answers that students commonly confuse with the correct answer
- Ensuring all options are similar in length
- Using your own words when you create the questions
- Avoiding options that give a clue to the answer or add irrelevant material
A fun way to use multiple-choice questions comes from an example in the book eLearning Course Creation for Beginners, by the League of Extraordinary Internet Marketing.
If you’re teaching a language, try using pictures instead of questions in your multiple-choice quiz. Underneath each picture, give the student three different definitions to choose from to identify what’s in the picture.
This is a good way to vary your questions, without really changing up the question type.
If you want to go deeper on how to write great multiple-choice questions, Vanderbilt’s Center for Teaching has a great guide on this.
True/False Quiz Questions
True/false questions are my least favorite type of quiz question because there’s a 50% chance your student will get it right, even if they guess. In my opinion, this gives you a poor opportunity to see whether your student is actually learning, but it does give you some insight.
These types of questions usually have a single statement that is either true or false, and the student has to choose which is correct. They’re used to see how familiar your student is with the content you’re teaching. They are also much easier to quickly scan to evaluate a student’s learning progress.
If you want to spice up your true/false questions a bit more though, you can always add in a relevant situation, and ask if that situation is correct.
For example:
Sally is performing keyword research on the term “wedding flowers”. Her first step is to enter this keyword into Keyword Finder. Is Sally correct? (T/F)
At the end of the day, regardless of the question type you choose, make sure you’re varying up the style. If you have all multiple-choice questions or all short-answer questions, some students might find it harder to stay engaged. Switching things up between lessons will help them stay engaged for longer.
How Often Should You Quiz?
There’s no hard and fast rule for how often you should quiz in your online course — it should be often enough to challenge your students adequately, and collect feedback on their learning progress. So whatever that means to you will work just fine.
I find it more effective to put a quiz at the end of each lesson so students feel like they can retain and recall what they’ve just learned.
But if a quiz at the end of each lesson is too much, try including a quiz after each module instead. I’d also recommend adding a short quiz at the beginning and end of your course so you can evaluate each student’s progress when they’re done. This will give you great feedback so you can improve your online course down the line.
Andrew Hubbard, a Facebook Ad Strategist, does this in his Amplified Ads course.
In his Welcome module, he asks students three questions that are more like getting-to-know-you questions. He asks students where they're from, what they do, and why they chose his course.
These aren't exactly quiz questions, but they're similar to what you can ask to get an idea of where your students are at before they dive into your course. That way you can evaluate how much they've learned by the end of it.
Wherever you put your quiz questions, keep their placement consistent so your students know what to expect.
Resources for Creating a Quiz in Your Online Course
I’m a big-time fan of course creator Facebook communities like Thinkific to stay up to date on what resources course creators are using to make their courses great.
When I was doing research for this post, I stumbled upon a few quiz resources that people have seen success with.
Quizlet: Quizlet lets you create quizzes and integrate them into platforms like Thinkific.
Brillium: Brillium lets you create powerful assessments in your online course, and integrates with all major Learning Management Systems.
H5P: H5P allows you to create and share interactive content in your course. It was recommended by a course creator in the Thinkific Facebook group who uses it for interactive quizzes.
Typeform: Some people are huge fans of Typeform, and have seen great success using it as a quiz in their online course. Thinkific has an entire blog post on how to integrate Typeform as a quiz into their platform.
Summary
Quizzes in your online course shouldn’t be an afterthought. Give them as much thought as you would your online course content. Ultimately, quizzes are what will determine if your students are learning anything you’re teaching, and give you great insight into how you can make your course better.
Here’s a quick rundown of what we covered on how to create a great quiz in your online course (that doesn’t suck!):
- A good quiz measures whether your student learned anything from your course and whether they learned enough.
- Good quiz questions relate back to your overall learning objectives.
- The most effective quiz questions let your students think critically, demonstrating their knowledge and creativity.
- The least effective quiz questions are questions that let students make educated guesses (like true/false or multiple-choice questions).
- There’s no hard and fast rule for how often you should quiz, but wherever you include your quiz questions, include them consistently (i.e., at the end of every lesson or module).
- Put thought into your quizzes! Take some time upfront to make sure they will accurately reflect whether your student is learning.
Are you already using quizzes in your course? How are you using them? Are you using any of the resources we mentioned? Let me know in the comments!




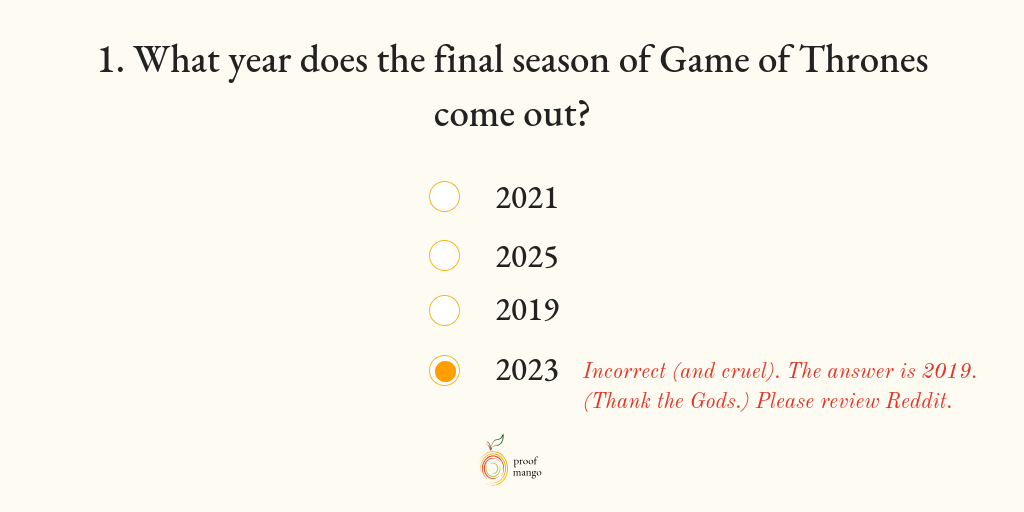

Pingback: The 10 Best Online Course Creators for 2020 - Mirasee
Pingback: How to Create Online Courses: The Ultimate Guide for Course Creators - Mirasee